

In a previous post I wrote an introduction to using the Alloy software modeling tool. In this post, I will use Alloy to solve two riddles, and introduce some more features of the Alloy language.
I will construct a model to solve the following riddle. It was found on the website Math is Fun.
This model will attempt to solve this riddle:
Four people are traveling to different places on different types of transport.
Their names are: Rachel, John, Mr. Jones and Cindy.
They either went on train, car, plane or ship.
Mr. Jones hates flying
Cindy has to rent her vehicle
John gets seasick
How did they each travel?
To begin, I created a signature to represent the people in the riddle, Rachel, John, Mr. Jones and Cindy. This class contains a relationship to a mode of transportation.
abstract sig People
{
//Mode of transportation
mode: disj one Transport
}
Here, the disj keyword says that the mode relationship is disjoint (unique) among People; that is, each mode of transportation only appears in one person's mode set at a time. Next, a signature was added for each person.
one sig Rachel extends People {}
one sig John extends People{}
one sig Jones extends People{}
one sig Cindy extends People{}
The one keyword here indicates that only one atom of the given signature may exist in the universe. Because People is abstract, the only People atoms that can exist are those that extend People. Because each individual is marked with the one keyword, the only possible People atoms that may exist in the universe are the 4 representing the 4 people in the riddle. Next, the same concept was applied to the modes of transportation:
//This signature represents modes of transport
abstract sig Transport {}
one sig Ship extends Transport {}
one sig Car extends Transport{}
one sig Plane extends Transport{}
one sig Train extends Transport{}
The next step is to capture the clues from the riddle as facts about the model. First, Mr. Jones hates flying, so one can assume Plane is not Mr. Jones' mode of transportation.
fact
{
all p: Plane | p not in Jones.mode
}
Next, Cindy had to rent her vehicle. This implies that Cindy's mode of transportation was a rental car.
fact
{
Cindy.mode = Car
}
John gets seasick, so John's mode of transportation would not be the ship.
fact
{
Ship not in John.mode
}
Running the model yields three possible results that satisfy the above constraints:
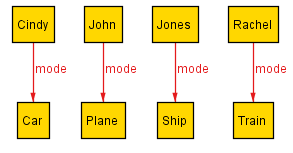
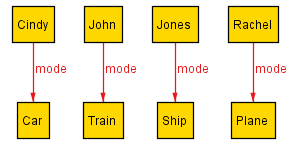
These generated outputs match the original solution.
There are 3 possibilities:
Cindy: car
Mr. Jones: train
John: plane
Rachel: ship
Cindy: car
Mr. Jones: ship
John: plane
Rachel: train
Cindy: car
Mr. Jones: ship
John: train
Rachel: plane
I will construct a model to solve the following riddle, also taken from Math is Fun.
I have three special four-sided dice.
They have one letter on each side.
When I roll them together I get three random letters which I try to rearrange into a word. In my eight goes so far I have made the words:
CAT, SON, POD, RIG, PEG, TAP, DIN, APE
What are the letters on each dice?
First, I followed the same abstract + singleton method above to create a signature for each of the letters that appear in the clue words above.
//Possible letters from the clue words
abstract sig Letters {}
one sig A extends Letters{}
one sig C extends Letters{}
one sig D extends Letters{}
one sig E extends Letters{}
one sig G extends Letters{}
one sig I extends Letters{}
one sig N extends Letters{}
one sig O extends Letters{}
one sig P extends Letters{}
one sig R extends Letters{}
one sig S extends Letters{}
one sig T extends Letters{}
Next I created a signature to represent a die. Each die has a set of letters. I used the disj keyword to enforce the constraint that no two die share the same set of letters. I added a constraint to the end of the signature declaration to specify that the number of letters must be 4, per the riddle.
//This represents a die
sig Die
{
//The set of letters, unique to each die
letters: disj set Letters
}
{
//Each die has 4 letters
#letters = 4
}
The second bracketed section that contains the #letters = 4 constraint is short-hand for a normal fact block; i.e. it is equivalent to writing:
fact
{
#Die.letters = 4
}
Alloy infers the reference to Die in the shorthand syntax because the block is appended to the Die signature declaration.
Next, a constraint was added to indicate that all members of the Letters class must be in the set of letters on a Die atom.
//All letters must be on a die
fact{
all l: Letters | l in Die.letters
}
It is worth noting that I did not explicitly set the cardinality of the Die class. Per the riddle, there are only three dice. This is implicitly enforced because the entire universe of the Letter set is explicitly declared with 12 letters, and the constraint on the number of letters per Die, 4, means that only three dice can exist.
To model the action of rolling the three dice, a predicate was created. In Alloy, a predicate is a block of logic that may take arguments and returns a Boolean True or False value. Alloy also has functions that have other types of return values, such as sets. The predicate looks like this:
pred roll[disj l, ll, lll: Letters]
{
some disj d, dd, ddd: Die |
l in d.letters &&
ll in dd.letters &&
lll in ddd.letters
}
The pred keyword specifies that this block is a predicate. The argument list to the predicate is defined inside the brackets []. The argument list is a bounding expression similar to those used in facts. In this case, the predicate takes three disjoint (unique, as specified by the disj keyword) Letter atoms, assigned to the variable names l,ll,lll. This is an admittedly lazy naming convention. They could be called anything, such as letter1,letter2, and letter3, etc. It is important to note that this predicate could be called with any set of three disjoint letters. In fact, Alloy may attempt every possible combination of letters in order to satisfy the model constraints (outlined below). The inner part of the predicate is the logical expression that resolves to either True or False. In this case, the bounding expression looks at three disjoint Die atoms, and enforces that atom l appears in d, ll appears in dd and lll appears in ddd. Just as the argument list to the predicate, d,dd, and ddd can be any set of three die selected form the universe of Die atoms. Essentially this predicate says "There exists some set of three unique die in which letter 1 appears in one of the die, letter 2 appears in another die, and letter 3 appears in the final die". The ordering here isn't important. Unlike a normal function call in a programming language, this predicate can (and likely will) be evaluated with every possible combination of letters and die in an attempt to find a combination that satisfies the conditions.
We are given a set of words as clues in the riddle. Therefore, we can state that there must exist a roll of three die that results in each of those words. Formally: there must exist some set of dice that satisfy the roll predicate when it is evaluated with the specified input letters. For example, the word "CAT" is given in the riddle. That means roll[C, A, T] must evaluate to True. Because the predicate specifies that each letter must come from a disjoint die, this implies that there exist three die, one of which contains C, another that contains A, and the final that contains T. This can be placed as a constraint on the model through a fact:
fact
{
roll[C, A, T]
}
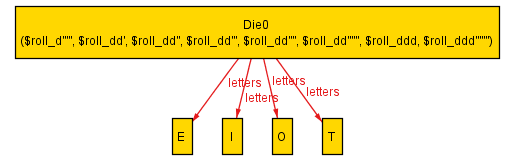
Executing this model results in an instance in which there are three dice, Die 0 that contains T, Die 1 that contains A and Die 2 that contains C:
The remaining clues can be enforced as constraints in the same way. Note the logical AND && combining the following expressions:
fact
{
roll[C, A, T] &&
roll[S, O, N] &&
roll[P, O, D] &&
roll[R, I, G] &&
roll[P, E, G] &&
roll[T, A, P] &&
roll[D, I, N] &&
roll[A, P, E]
}
Executing this model results in a single solution in which all of the above rolls can be satisfied:
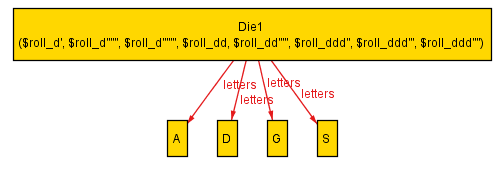
The original solution matches the solution Alloy generated:
The letters on the three dice are:
CNPR AGDS EIOT
/*
This model will attempt to solve this riddle:
Four people are traveling to different places on different types of transport.
Their names are: Rachel, John, Mr. Jones and Cindy.
They either went on train, car, plane or ship.
Mr. Jones hates flying
Cindy has to rent her vehicle
John gets seasick
How did they each travel?
https://www.mathsisfun.com/puzzles/four-people-travel-solution.html
*/
//This signature represents people
abstract sig People
{
//Mode of transportation
mode: disj one Transport
}
//These signatures represent individuals
one sig Rachel extends People {}
one sig John extends People{}
one sig Jones extends People{}
one sig Cindy extends People{}
//This signature represents modes of transport
abstract sig Transport {}
one sig Ship extends Transport {}
one sig Car extends Transport{}
one sig Plane extends Transport{}
one sig Train extends Transport{}
//Mr. Jones hates flying => Plane is not in Jones' mode set
fact
{
Plane not in Jones.mode
}
//Cindy has to rent her vehicle => Cindy's set only includes car
fact
{
Cindy.mode = Car
}
//John gets seasick => John did not travel by boat
fact{
Ship not in John.mode
}
//Executing this results in one of exactly 3 possible models. Using the "new" button
//will cycle through the 3 possibilities. Per the original webiste:
//
//https://www.mathsisfun.com/puzzles/four-people-travel-solution.html
//
//The possible solutions are:
/*
Cindy: car
Mr. Jones: train
John: plane
Rachel: ship
Cindy: car
Mr. Jones: ship
John: plane
Rachel: train
Cindy: car
Mr. Jones: ship
John: train
Rachel: plane
*/
run {}
/*
This model will attempt to solve this riddle:
I have three special four-sided dice.
They have one letter on each side.
When I roll them together I get three random letters which I try to rearrange into a word. In my eight goes so far I have made the words:
CAT, SON, POD, RIG, PEG, TAP, DIN, APE
What are the letters on each dice?
https://www.mathsisfun.com/puzzles/four-sided-dice.html
*/
//Possible letters from the clue words
abstract sig Letters {}
one sig A extends Letters{}
one sig C extends Letters{}
one sig D extends Letters{}
one sig E extends Letters{}
one sig G extends Letters{}
one sig I extends Letters{}
one sig N extends Letters{}
one sig O extends Letters{}
one sig P extends Letters{}
one sig R extends Letters{}
one sig S extends Letters{}
one sig T extends Letters{}
//This represents a die
sig Die
{
//The set of letters, unique to each die
letters: disj set Letters
}
{
//Each die has 4 letters
#letters = 4
}
//All letters must be on a die
fact{
all l: Letters | l in Die.letters
}
//This predicate represents a roll
pred roll[disj l, ll, lll: Letters]
{
some disj d, dd, ddd: Die |
l in d.letters &&
ll in dd.letters &&
lll in ddd.letters
}
/*
This fact specifies the rolls provided in the riddle clues
*/
fact
{
roll[C, A, T] &&
roll[S, O, N] &&
roll[P, O, D] &&
roll[R, I, G] &&
roll[P, E, G] &&
roll[T, A, P] &&
roll[D, I, N] &&
roll[A, P, E]
}
//Running this model results in the solution:
//CNPR AGDS EIOT
// https://www.mathsisfun.com/puzzles/four-sided-dice-solution.html
run {}
I think these riddle models are a fun way to practice modeling with Alloy and a good method for introducing some of the features of the Alloy language. I intend to continue demonstrating Alloy features in future posts.